بسیاری فکر میکنند ریاضیات اختراع انسانها است و به آن به چشم یک زبان نگاه میکنند؛ این زبان چیزهایی را از دنیای واقعی توصیف میکند که بیرون از ذهن کسانی که به آن زبان صحبت میکنند “وجود” ندارد.
اما مکتب فیثاغورث در یونان نظر دیگری داشت. طرفداران این مکتب معتقد بودند ریاضیات، اساسِ واقعیت است. بیش از دو هزار سال از این ایده میگذرد و ظاهراً این ایده، کمکم توسط فیلسوفان و فیریکدانان جدی گرفته میشود.
ریاضیات جزء ضروری طبیعت است. ریاضیات چیزی است که به جهان مادی ساختار میبخشد.

زنبورها کندوهایشان را به شکل شش ضلعی میسازند. چرا؟
بر اساس تئوری “لانه زنبوری” در ریاضیات، شش ضلعیها بهترین شکل برای کاشیکاری یک سطح هستند. اگر بخواهید سطحی را با استفاده از کاشیهایی با شکل و اندازه مشابه به طور کامل بپوشانید و طول محیط را به حداقل برسانید، شش ضلعیها بهترین انتخاب ممکن هستند.
چارلز داروین استدلال کرد که زنبورها برای استفاده از این شکل تکامل یافتهاند چون میخواهند بزرگترین سلولها را برای ذخیره عسل با کمترین انرژی و موم ممکن بسازند.

تئوری لانه زنبوری برای اولین بار در زمانهای بسیار دور مطرح شد و در سال 1999 توسط توماس هیلز که یک ریاضیدان است به اثبات رسید.
حال میخواهیم یک مثال دیگر بزنیم. دو زیرگونه از جیرجیرکهای دورهای آمریکای شمالی وجود دارند که بیشتر عمر خود را در زمین میگذرانند. سپس هر 13 یا 17 سال یک بار (بسته به زیرگونهشان) در دستههای بزرگ در سطح زمین پدیدار میگردند.
اما چرا 13 و 17؟ چرا در دورههای 12، 14، 16 یا 18 ساله این اتفاق نمیافتد؟
یک توضیح منطقی میتواند این باشد که هر دوی این اعداد، اول هستند.

تصور کنید که این جیرجیرکها شکارچیانی دارند که آنها هم بیشتر عمر خود را در زمین میگذرانند. این جیرجیرکها باید زمانی که شکارچیانشان زیرزمین خواب هستند، بیرون بیایند.
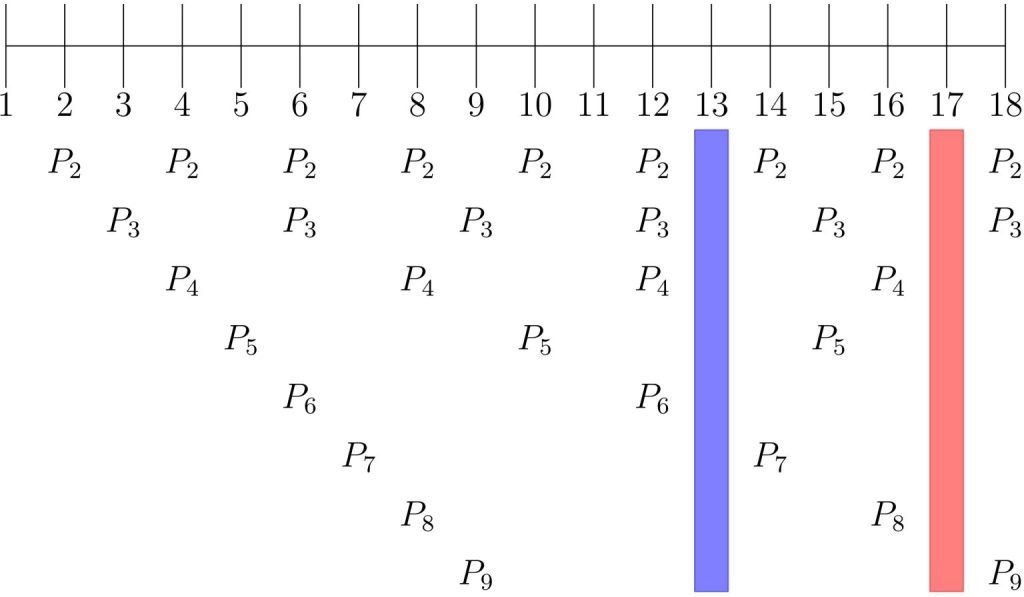
تصور کنید که این شکارچیان دورهای که در زیر زمین میگذرانند 2، 3، 4، 5، 6، 7، 8 یا نه سال باشد. چطور میتوان از رویارویی با تک تک آنها اجتناب کرد؟
بیایید دوره 12 ساله و 13 ساله را با هم مقایسه کنیم. اگر جیرجیرکها هر 12 سال یکبار بر روی زمین بیایند، شکارچیانی که دوره 2، 3، 4 ساله دارند نیز در سطح زمین هستند. زیرا دوازده بر 2، 3 و 4 بخشپذیر است.
اما زمانی که جیرجیرکها هر 13 سال یک بار به سطح زمین بیایند هیچکدام از این شکارچیان در سطح زمین نیستند. زیرا 13 به هیچکدام از این اعداد بخشپذیر نیست. این قضیه برای دوره هفده ساله هم درست است.
به نظر میرسد این جیرجیرکها برای بهرهبرداری از این مسئله ریاضی، تکامل یافتهاند.
زمانی که شروع به جستجو کنید، پیدا کردن موارد مشابه آسان میشود. از شکل لایههای صابونی گرفته تا طراحی چرخدنده موتور یا حتی اندازه و محل شکافهای حلقههای زحل، ریاضیات همه جا وجود دارد.
اگر ریاضیات بسیاری از چیزهایی که ما در اطراف خود میبینیم را توضیح میدهد، پس بعید است چیزی باشد که ما اختراع کرده باشیم. حقایق ریاضی کشف میشوند. نه تنها توسط انسان بلکه توسط حشرات، حبابهای صابون، موتور احتراق و سیارات!
اما اگر ما در حال کشف چیزی هستیم، آن چیست؟
افلاطون، فیلسوف معروف یونانی، پاسخی برای این سوال داشت. او میگفت ریاضیات چیزهایی را توصیف میکند که واقعا وجود دارند.
برای افلاطون آن چیزها، اعداد و اشکال هندسی بودند. امروزه ما اشیا ریاضی پیچیدهتری مثل گروهها، دستهها، توابع، میدانها، و حلقهها را میتوانیم به تعریف افلاطون اضافه کنیم.

افلاطون همچنین معتقد بود که اشیا ریاضی خارج از فضا و زمان وجود دارند. اما چنین دیدگاهی این معما را پیچیدهتر میکند که چطور ریاضیات هر چیزی را توضیح میدهد.
این توضیحات نشان میدهند که چگونه یک چیز در جهان به چیزی دیگر بستگی دارد. اگر ریاضیات در قلمرویی جدا از قلمروی دنیای واقعی وجود میداشت، با هیچ چیزی در این دنیا نمیتوانست ارتباطی برقرار کند.
طرفداران فیثاغورث در آن زمان با افلاطون موافق بودند و آنها نیز میگفتند که ریاضیات دنیایی از اشیاء را توصیف میکند. اما برخلاف افلاطون آنها فکر نمیکردند که اشیاء ریاضی فراتر از مکان و زمان وجود داشته باشند. در عوض آنها معتقد بودند که همانگونه که ماده از اتمها ساخته شده، واقعیتهای فیزیکی نیز از ریاضیات ساخته شده است.
اگر واقعیت از اشیاء ریاضی ساخته شده باشد، به راحتی میتوان توضیح داد که چگونه ریاضیات ممکن است در توضیح جهان پیرامون ما نقش داشته باشد.
در دهه گذشته، دو فیزیکدان مدافع سرسخت نظرات فیثاغورث بودهاند. کیهانشناس سوئدی–آمریکایی مکس تگمارک و فیزیکدان–فیلسوف استرالیایی، جین مک دانل.
تگمارک معتقد است که واقعیت فقط یک شی بزرگ ریاضی است. اگر عجیب بنظر میرسد به این فکر کنید که واقعیت ممکن است یک شبیهساز ریاضی باشد. حتی در آن صورت هم شبیهساز، یک برنامه کامپیوتری است و به نوعی یک شی ریاضی محسوب میشود!
دیدگاه مک دانل افراطیتر است. او فکر میکند واقعیت از اشیاء و ذهنهای ریاضی تشکیل شده است.
یک دیدگاه دیگر نیز وجود دارد. جهان دو بخش دارد. ریاضیات و ماده. ریاضیات به ماده شکل داده و ماده به ریاضیات استحکام میبخشد.
اشیاء ریاضی چارچوبی برای دنیای مادی فراهم میکند.
منطقی است اگر فکر کنیم تفکر فیثاغورث دارد دوباره به فیزیک برمیگردد. در قرن گذشته، فیزیک روزبهروز محاسباتیتر و ریاضیاتیتر شده است و در تلاش برای توضیح جهان مادی، به حوزههای انتزاعی ریاضیات مانند نظریه گروهها و هندسه دیفرانسیل روی آورده است.
با توجه به اینکه هر روز مرزهای بین فیزیک و ریاضیات کمرنگتر میشوند، سخت است که بگوییم کدام بخش از جهان ریاضیاتی و کدام فیزیکی است.
عجیب است که این همه مدت تفکرات فیثاغورثی توسط فیلسوفان نادیده گرفته شده است. به نظر میرسد این اوضاع در حال تغییر است. زمان انقلاب فیثاغورثی فرا رسیده، انقلابی که قرار است درک ما را از واقعیت به کلی تغییر دهد.
منبع: Scitechdaily






























